조건부 확률 : 전체 확률에 조건(scope)를 만드는 것
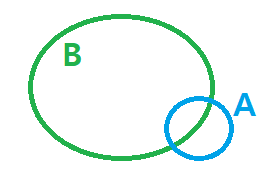
B라는 조건(scope)안에 A가 발생할 확률은 다음과 같다.


이며, 1번식에 의해,

이므로, 2번식은 다음과 같이 정리된다.

또한 조건부 확률에는 다음과 같은 특성이 있으며 자주 쓰인다.

Probability Distribution : 어떤 이벤트가 발생되었을 때 값을 할당하는 것(A function mapping an event to a probability)

이 때 x는 event가 들어간다.
ex) x = 3일 때의 확률, x = 5일 때의 확률. 즉, x는 certain point.
parameter나 f(x)를 바꿈으로써 확률 값을 변경할 수 있다.
이 때, normal distribution에선,

이 때, Notation = N(mu, sigma^2), Mean : mu, Variance : sigma^2 이다.
확률을 모델링하는 방법 : Beta Distribution(1.3에 쓰인 방법)




이 때 alpha, beta가 parameter이다.
Binomial Distribution: Simplest distribution for discrete values
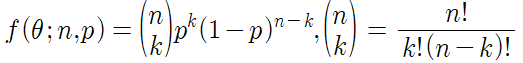
이 때 paramter는 n과 p이며,

beta와 normal은 부드러운 선인데, binomial은 점이 뚝뚝 끊어진 형태이다. 즉, discrete한 event에 대한 확률을 정할 때 쓰는 방식이다.(1.5번, 1.75번을 던질 수 없다.)
binomial은 두번의 경우인데, 경우의 수가 3개, 4개라면 multinomial distribution이 필요하다.
Word selection, cluster selection와 같은 경우에서 쓰일 수 있다.
'컴퓨터 > 인공지능 및 기계학습 개론1' 카테고리의 다른 글
| 2.2. Introduction to Rule Based Algorithm (0) | 2021.01.23 |
|---|---|
| 2.1. Rule Based Machine Learning Overview (0) | 2021.01.23 |
| 1.3. MAP (0) | 2021.01.23 |
| 1.2 MLE (0) | 2021.01.22 |
| 1.1 Motivations (0) | 2021.01.22 |

