Linear Regression(회기 분석)
Introduction to Linear Regression
Housing Information : 13개의 continuous variable(independent values), 1개의 true value(dependent value)로 이루어져있다.
function approximation을 linear한 형태 function으로 approximation하는 것이 linear regession이다.
이전까지는 hypothesis를 rule로 정의했지만, 이번에는 function으로 정의한다.

θ zero에 linear sum을 더한 것으로 dependent variable을 정의한다.
θ를 잘 정하면 잘 approximation 될 것이다.
이 때, n = independent value의 개수, linerly wieght sum과 θ가 있다.
Finding Parameter in Linear Regression
θ zero를 1로 하여 dummy data처럼 만든다.

현실에선 error가 있는데 이 error을 포함한 것이 true parameter이다.
(위에서 f hat을 한 이유는 가짜임을 표현하기 위함)
True Y라는 것은 Xθ + e이다.
X는 data로 정의되어 있고, 목표는 e를 줄이고 θ를 늘리는 것이다.
argmin : minimize 시켜주는 θ를 만들어서 그것을 θ hat이라고 잡겠다. 여기서 제곱은 에러에 패널티를 주는 것.
Y는 관측된 값으로 independnet variable, X는 dependent variable이다.
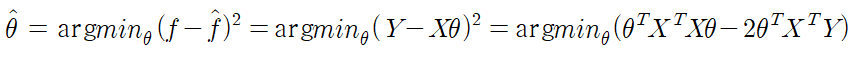
이 값을 미분하여 정리하면 θ는 다음과 같다.

이 때 X를 뻥튀길 할 수록 실제 값에 더욱 가까워진다. 단, 더이상 linear 되지 않는다.
또한, 승수를 높여가며 만든 곡선이 미래의 값에도 통하는지는 의문스럽다.
Limitations
심플하면 고장나지 않고, 오류가 적기 때문에 많은 곳에서 사용될 수 있다.
하지만 많은 데이터를 기반으로 training, paramter 대입 등에선 한계점이 분명히 존재한다.
>> 데이터가 많아질수록 억지스러운 듯 모델이 복잡해지고, 에러가 늘어날 수 있다.
하지만 분명히 기초가 되는 모델임을 분명하다.
'컴퓨터 > 인공지능 및 기계학습 개론1' 카테고리의 다른 글
| 3.3. Naive Bayes Classifier (0) | 2021.01.24 |
|---|---|
| 3.1. Optimal Classification (0) | 2021.01.24 |
| 2.4. Entropy and Information Gain (0) | 2021.01.23 |
| 2.3. Introduction to Decision Tree (0) | 2021.01.23 |
| 2.2. Introduction to Rule Based Algorithm (0) | 2021.01.23 |